Linear Systems
Beloved, I pray that you may prosper in all 'good' things and be in good health, even as thy soul prospers.
- 3rd John 1:2
The Joy of a Teacher is the Success of his Students.
- Samuel Dominic Chukwuemeka
I greet you this day,
ALEKS Software for the homework assignments
Please:
(1.) Visit the website: ALEKS - Student Registration and
sign up for ALEKS.
Register with only the First Name and Last Name on the Canvas course as is.
No nicknames. No shortened names.
Your First Name and Last Name on ALEKS should exactly match your
First Name and Last Name on Canvas.
(2.) Review this information:
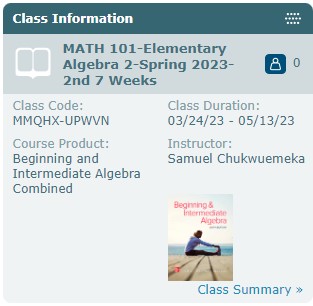
(3.) This is the textbook for the class.

It comes with an access code.
The access code contains the eBook (soft copy). The access code is required.
The printed copy (hard copy) is optional.
If you decide to purchase the printed copy of the textbook from the Bookstore or from anywhwere, please ask them to
include the access code for you.
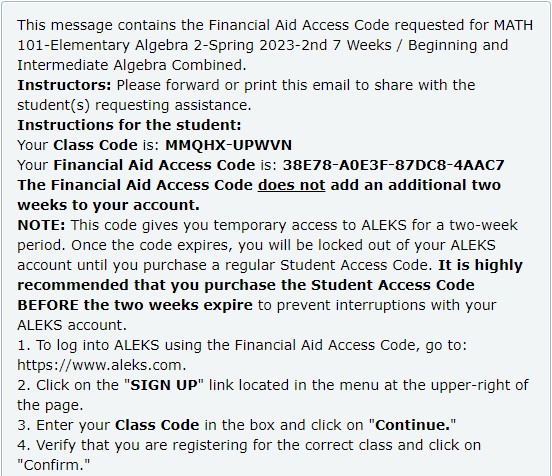
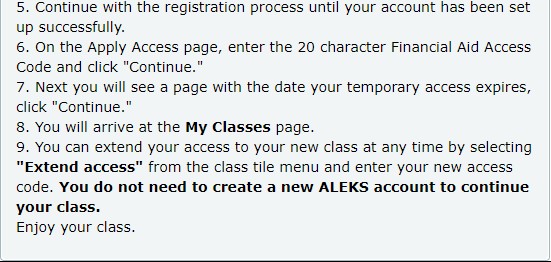
(4.) Financial Aid Access Code: (Free for Two Weeks)
For students who: did not receive financial aid
and do not have the funds to purchase the code right now but intend to purchase it later and want to
begin the homework assignments immediately, please review:
(5.) Follow the steps listed here (Video):
ALEKS Student Registration Video
(6.) Alternatively, you may follow the steps listed here (Written):
(7.) Begin your homework assignments.
First: read the notes.
Second: view the videos.
Third: solve the questions/solved examples.
Fourth: check your solutions with my thoroughly-explained solutions.
| Midterm Exam Study Guide | Final Exam Study Guide |
|---|---|
|
(1.) Overview of Linear Systems
(2.) Graphical Solution of Linear Systems (3.) Solution of Linear Systems by Substitution (4.) Solution of Linear Systems by Elimination (5.) Word Problems on 2 by 2 Linear Systems (6.) Exponential Expressions |
(1.) Overview of Linear Systems
(2.) Graphical Solution of Linear Systems (3.) Solution of Linear Systems by Substitution (4.) Solution of Linear Systems by Elimination (5.) Word Problems on 2 by 2 Linear Systems (6.) Exponential Expressions (7.) Arithmetic Operations on Polynomials (8.) Factor Polynomials (9.) Solution of Quadratic Equations (10.) Application of Quadratic Equations |
Fifth: check your answers with the
calculators as applicable.
Comments, ideas, areas of improvement, questions, and constructive criticisms are welcome. You may contact me.
If you are my student, please do not contact me here. Contact me via the school's system.
Thank you for visiting.
Samuel Dominic Chukwuemeka (SamDom For Peace)
B.Eng., A.A.T, M.Ed., M.S
